
La relatividad de Einstein: Contracción y el tiempo relativo – 3
Dijimos que la genialidad de Einstein fue asociar este fenómeno a la función coseno (Factor de Lorentz).
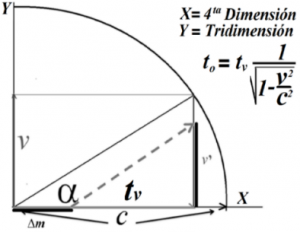
Para la comprensión del factor de Lorentz, pensemos en un triángulo rectángulo ideal, con lados 3, 4, 5 (“v“, “T“, “c“, respectivamente, fig. 1). Un móvil con movimiento relativo “v” = 3/5 (con velocidad 3/5 de “c”, 180.000 km/s).
La coordenada “Y” representa a la tridimensión (lo que vemos); y la coordenada “X” representa a la 4ta dimensión (“expansión del universo”), donde a es el cambio de dirección de la onda-partícula (trayecto real del móvil) en la 4ta dimensión. En el ejemplo, el coseno a es 0,8, por (5) “c“, es igual a “4”= “Tv“, de donde será √ [1-(32/52)], la raíz de: 1 menos (32 dividido 52); 1-(9/25); 1- (36/100)= 1-0,36 = 0,64, cuya raíz es 0,8, que por la hipotenusa (5) = 4 = “Tv“.
En términos prácticos
Supongamos una nave espacial, con velocidad ” v ” (3/5 c, 180.000 km/s) hacia una estrella a 10 años luz, a esa velocidad le tomaría t =16,7 años en llegar (para el observador en la Tierra), pero el tripulante encontrará, que llegará a la estrella en un tiempo t = 13,3 años (“0,8” del tiempo que tendría que haber utilizado).
Para él (viajero), el espacio se contrajo, porque su tiempo no es igual. Vemos que, para llegar a la estrella, tendría que haber usado casi 17 años, viajando a esa velocidad (3/5 “c”, 180.000 Km/s), pero llega en algo más de 13 años, porque el espacio se contrajo (para él), aunque para quien quedó en la Tierra, demoró casi 17 años. Y ve que al viajero, el tiempo le pasa más lento.
Si pudiésemos ver al viajero saludando (con la mano), veríamos que levanta la mano muy lento, no porque lo hace lento, sino porque su tiempo es diferente.
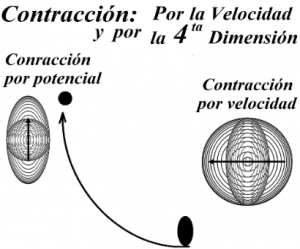
Contracción del cuerpo
Imaginemos ahora una bola en velocidad, sobre una superficie plana. Para la Teoría Relatividad Especial (TRE, § 4, 1905), tendría una contracción en el sentido de la velocidad, viéndose elipsoide (achatada, ver figura 2), de acuerdo a la velocidad de la información. La contracción del espacio es en la dirección de la velocidad.
Al subir una rampa: La bola en la rampa se “achatará” en sentido “perpendicular”, volviendo a ser una esfera (más pequeña). Esta es la contracción por la energía en la 4ta dimensión (“m”). La bola será una esfera más pequeña, y con más masa. Sin velocidad relativa.
La razón matemática
La forma geométrica de ver el fenómeno: Para que pierda velocidad sin perder energía en la rampa; si tiene la misma dirección y menos velocidad, es necesario que se desplace el origen (vértice) del ángulo a, explicando el cambio de lugar en la 4ta dimensión (“x”), v’ menor espacio en igual tiempo (“c”, del observador).
Esta es la masa, que es equivalente con la energía: E=mc2. La contracción por un potencial (que es absoluta), determina el lugar en la 4ta dimensión del cuerpo (partícula, etc.); no como Einstein proponía por el factor de Lorentz, ya que, en su perpendicular tendría que tener otra masa inercial. Esto lo veremos más adelante.
Continuará…
“El corazón del entendido adquiere sabiduría; y el oído de los sabios busca la ciencia.” Prov. 18:15




Deja tu comentario